Dyfrakcja to zjawisko fizyczne zmiany kierunku rozchodzenia się fali na krawędziach przeszkód oraz w ich pobliżu. Zjawisko zachodzi dla wszystkich wielkości przeszkód, ale wyraźnie jest obserwowane dla przeszkód o rozmiarach porównywalnych z długością fali.
Dyfrakcja używana jest do badania fal oraz obiektów o niewielkich rozmiarach, w tym i kryształów, ogranicza jednak zdolność rozdzielczą układów optycznych.
Jeżeli wiązka fal przechodzi przez szczelinę lub omija obiekt, to zachodzi zjawisko ugięcia. Zgodnie z zasadą Huygensa fala rozchodzi się w ten sposób, że każdy punkt fali staje się nowym źródłem fali, tak powstałe fale rozchodzą się jako fale kuliste, a fala w każdym punkcie jest sumą wszystkich fal (interferencja). Za przeszkodą pojawią się obszary wzmocnienia i osłabienia rozchodzących się fal.
Zjawisko dyfrakcji występuje dla wszystkich rodzajów fal np. fal elektromagnetycznych, fal dźwiękowych oraz fal materii.
Jeden z najprostszych przykładów zjawiska dyfrakcji zachodzi, gdy równoległa wiązka światła (np z lasera) przechodzi przez wąską pojedynczą szczelinę zwaną szczeliną dyfrakcyjną. Zgodnie z zasadą Huygensa każdy punkt szczeliny o szerokości d, jest nowym źródłem fali. Między źródłami zachodzi interferencja, co powoduje wzmacnianie i osłabianie światła rozchodzącego się w różnych kierunkach. Dla pojedynczej szczeliny jasność w funkcji kąta odchylenia od osi przyjmuje postać:
-
![I(\theta) =I_0 {\left[ \operatorname{sinc} \left( \frac{\pi d}{\lambda} \sin \theta \right) \right] }^2](http://upload.wikimedia.org/math/e/b/b/ebb905a66b0311535ec01de8d5f30f49.png) ,
,
gdzie:
- I – intensywność światła,
- I0 – intensywność światła w maksimum, czyli dla kąta równego 0,
- λ – długość fali,
- d – szerokość szczeliny,
- funkcja sinc(x) = sin(x)/x.
Przepuszczenie fali przez szczelinę dyfrakcyjną pozwala na określenie kierunku rozchodzenia się fali. Im mniejsza jest szerokość szczeliny, tym dokładniej można to zrobić. Jednocześnie zmniejszanie szczeliny powoduje, że trudniej jest określić energię fali, ponieważ rozprasza się ona na większy obszar. W efekcie iloczyn błędu określenia energii oraz błędu pomiaru kierunku musi być większy od pewnej stałej. Oznacza to, że istnieje granica dokładności pomiaru parametrów rozchodzącej się fali. Zjawisko to ma fundamentalne znaczenie, jeżeli weźmie się pod uwagę, że każda materialna cząstka jest falą. Zjawisko to jest potwierdzeniem zasady nieoznaczoności. Dualizm korpuskularno-falowy powoduje, że możliwa jest obserwacja dyfrakcji cząstek materialnych. Eksperymenty udowodniły, że zjawisko to zachodzi dla elektronów i neutronów
Aby wzmocnić falę przechodzącą przez szczelinę stosuje się w optyce układy wielu takich szczelin, nazywane siatką dyfrakcyjną. Efekty optyczne od każdej szczeliny dodają się, przez co zachowanie fali zależy tylko od stałej siatki (odległości dzielącej najbliższe sobie rysy).
Zjawisko dyfrakcji zachodzi również, kiedy fale przechodzą przez wiele blisko siebie położonych warstw. Jeżeli odległość między warstwami jest stała, kolejne maksima fali można opisać zależnością:
-
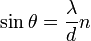 ,
,
gdzie:
- d – stała siatki,
- θ – kąt od osi wiązki światła,
- λ – długość fali,
- n – przyjmuje wartości całkowite dodatnie od 1,2,3,...
Dla promieniowania rentgenowskiego zjawisko to pozwala na obserwacje kolejnych warstw kryształu. W świetle widzialnym dyfrakcję na warstwach można obserwować jako rozproszenie światła białego na powierzchni płyty CD. Kolejne ścieżki tworzą następujące po sobie warstwy, na których fale o różnych kolorach, załamują się pod różnym kątem. W efekcie światło białe rozdziela się na poszczególne barwy.
Jeżeli prześledzimy zachowanie się fali, która omija przeszkodę mniejszą niż dwie długości fali, okaże się, że fala nie reaguje na tak mały obiekt. Fakt ten powoduje konieczność stosowania krótszych fal do obserwacji mniejszych przedmiotów. Aby obserwować strukturę krystaliczną materii, konieczne jest użycie fal rentgenowskich. Zjawisko dyfrakcji pozwoliło na rozwój krystalografii rentgenowskiej, dzięki której odkryto strukturę spirali DNA. W procesie produkcji układów scalonych wykorzystuje się światło do rysowania kształtu obwodu elektrycznego na podłożu. Zjawisko dyfrakcji zmusza producenta mikroprocesorów do zastosowania fal dwa razy krótszych niż konieczna precyzja struktury układu. Dla obwodów o dokładności 0,13 μm, oznacza to konieczność posłużenia się ultrafioletem. Jeżeli układy scalone mają się rozwijać zgodnie z prawem Moore'a, konieczne jest wdrożenie nowych technologii opierających się na falach mniejszej długości. Światło ulega największemu załamaniu w narożach i zakrętach ścieżek maski, więc konstruktorzy obecnie tak modyfikują maskę w narożach otworów i na zakrętach ścieżek, by zminimalizować dyfrakcję, długość światła dobiera się tak by pierwsze prążki interferencyjne równoległych ścieżek nie nakładały się, poprawiono własności emulsji. Po dokonaniu tych zmian ww kryterium długości fali udało się złagodzić.
